در سه قسمت قبلی فیزیک کلاسیک را به شکلی جامع بررسی کردیم، سپس به دنیای فیزیک کوانتوم گام نهادیم و نارسایی‌های متعدد فیزیک کلاسیک را شرح و تفسیر دادیم، اکنون به لزوم ایجاد فیزیکی جدید و اصول موضوعه‌ای نوین واقف هستیم. در این قسمت یک گام دیگر برای آشنایی بیشتر با فیزیک کوانتوم بر می‌داریم.

همان طور که در قسمت‌های قبلی این مجموعه مقالات نیز بیان کردیم، هدف و علاقه‌ی ما از نگارش این مجموعه مقالات، بیان روایتی جذاب و در عین حال قابل فهم است، تا مخاطبی که پایه‌ی ریاضیات محکمی ندارد و در عین حال علاقه‌مند به علم است نیز این از روایت لذت ببرد. گرچه بسیاری از مواقع ورود به ریاضیات اجتناب ناپذیر است.

با توجه به اینکه در قسمت قبلی، به فراخور مطلب استفاده از روابط ریاضیاتی الزامی بود، در نظر داشتیم در این قسمت بخشی از فیزیک نوین را برای شما روایت کنیم، که جذاب، پرکشش و در عین پیچیده بودن قابل تصور باشد و چه انتخابی بهتر از یک واقعه‌ی علمی که در خلال همان سال‌های داغ جدال فیزیک کلاسیک و نوین رخ داد؟

نظریه نسبیت اینشتین در ابتدا نه تنها درک نشد، بلکه مورد مخالفت جدی قرار گرفت، اما گذر زمان و پیشرفت فیزیک حقانیت و صحیح بودن آن را به اثبات رساند. نگارنده‌ی آن معروف‌ترین، شاخص‌ترین و شاید متفاوت‌ترین فیزیکدان قرن بیستم است، یعنی آلبرت اینشتین، مردی که در آلمان متولد شد به سوییس کوچ کرد و در نهایت در ایالات متحده آرام گرفت.  

نسبیت

نسبیت با یک پرسش معمولی آغاز می‌شود؛ هرگاه ما نسبت به یکدیگر در حال حرکت باشیم، فیزیک شما به فیزیک من چگونه مربوط می‌شود؟ گالیله چنین پاسخ می‌دهد؛ که اگر سرعت نسبی ما یکسان باشد، دقیقا قوانین مکانیک یکسانی را می‌یابیم. نیوتون همان چیز را می‌گوید، اما به تفصیل بیشتر با ارجاع همه حرکت‌ها (شما، من و هر کس دیگر) به چارچوب مرجع مطلق در فضا و زمان!

در قرن ۱۹ میلادی نظریه‌پردازان می‌پنداشتند، واسطه‌ی گسیل نور محیط با واسطه‌ای به نام اِتِر است، که فضا را پر می‌کند. آنان اعتقاد داشتند، که برای انتشار پرتو الکترومغناطیس، وجود محیط اتری لازم است. بر اساس این نظریه، نور آشوب اِتِر محسوب می‌شد که به موجب آن، اتم‌هایش به طرز خاصی مرتعش شده و موجب گسیل نور می‌شوند.

فیزیک اِتِر در میان دانشمندان دوره ویکتوریا مجاهدت برجسته‌ای بود، اما نقص‌های مهلکی داشت. از یک لحاظ، فیزیکدانانی که اِتِر را پذیرفته بودند، هرگز نتوانستند با یک مدل استاندارد برای ساختار مکانیکی اِتِر توافق داشته باشند. همچنین مفهوم حرکت در یک اِتِر با تکیه بر چارچوب مرجع مطلق نیوتون سؤال انگیز و قابل تردید بود. در سال‌های ۱۸۸۰ یک سری آزمایش‌هایی به منظور تشخیص حرکت زمین نسبت به یک دریای اِتِر به وسيله آلبرت مایکلسون و ادوارد مورلی انجام شد(برای مطالعه‌ی جزییات آن به قسمت اول رجوع کنید) که به ناکامی چشمگیری انجامید. واقعیت سرسختانه‌ای که همیشه مشاهده می‌شد، این بود که سرعت نور در فضای خالی، صرف نظر از سرعت و جهت چشمه نور، یکسان است.

یک مأمور تحقیق اداره ثبت اختراع در شهر برن سویس به نام آلبرت اینشتین در سال ۱۹۰۵ مقاله‌ای منتشر کرد، که مسئله‌ی اِتِر را به سادگی با نادیده گرفتن آن، حل می‌کرد. اینشتین دو اصل تجربی غیرقابل انکار را مسلم فرض کرد:

•  ثابت بودن سرعت نور
• تعمیمی از اصل نسبیت گالیله برای شمول پدیده‌های الکترومغناطیسی و اپتیکی.

 با شروع این دو اص، و بدون توسل به مفهوم اِتِر، او ثابت کرد برای ناظرانی که با سرعت‌های ثابت (متفاوتی) نسبت به یکدیگر حرکت می‌کنند، اندازه‌های طول و زمان متفاوت است و شاید هر چه سرعت به سرعت نور نزدیک‌تر باشد، این تفاوت شدیدتر خواهد بود. به طور مثال، اگر ناظر ساکنی مراقب ساعتی باشد، که با سرعت زیاد حرکت می‌کند، می‌بیند که این ساعت کندتر از وقتی تیک تاک می‌کند، که ناظری با ساعت در حرکت باشد.

 علاوه بر این تأخیر یا اتساع زمان، اینشتین در مقاله سال ۱۹۰۵ خود اصرار می‌ورزد که بُعد طول ساعت، یا هر چیز دیگر در جهت حرکت برای ناظر ساکن، منقبض می‌شود.

اینشتین در سال ۱۹۰۵ نظریه‌‌ی نسبیت خاص خود را با دو محدودیت مطرح کرد: این نظریه بر سیستم‌های لَخت (inertial) متمرکز بود، سیستم‌هایی که با سرعت‌های نسبی ثابت در حرکت بودند و گرچه این نظریه با معادلات ماکسول برای میدان الکترومغناطیسی سازگار بود، حوزه‌ی آن نظریه بزرگ دیگری از گذشته، یعنی نظریه نیوتونی را شامل نمی‌شد. اینشتین به زودی دریافت که یک نظریه‌ی عام نسبیت می‌باید، هم آثار گرانشی و هم سیستم‌های غیرلخت، یعنی سیستم‌هایی را که نسبت به یکدیگر شتاب دارند، مشخص کند. نخستین مرحله در آن جهت که بعدها اصل هم ارزی نامیده شد، تاکیدی بود بر بهترین اندیشه اینشتین که شتاب و گرانش عمیقا به یکدیگر مربوطند؛ جایی که شتاب وجود دارد و آثار گرانشی مصنوعی که از واقعی آن غیرقابل تمیز است نیز وجود دارد.

اینشتین همچنان که با اصل هم ارزی به عنوان رهنمون کارش پیش می‌رفت، به این آگاهی دست یافت که فضا و زمان به طور خاصی در سیستم‌های شتاب‌دار پیچیده شده‌اند؛ فرمول‌های اقلیدسی از جمله محاسبه نسبت محیط به قطر در دایره به عنوان عدد پی یا Π اندکی با خطا همراه است. این موضوع سر رشته‌ای حیاتی به او داد که نظریه‌ی عام نسبیت می‌باید، براساس هندسه‌ی غیر اقلیدسی باشد. از قضا، یک نظریه‌ی کامل فضاهای غیراقلیدسی، که در سال‌های ۱۸۵۰ به وسیله برنهارد ريمان بسط یافته بود، دقیقا ابزارهایی ریاضی را برای اینشتین فراهم آورد، تا بنای محکمی برای نظریه‌ای که هندسه و گرانش را به هم متصل می‌کرد، بسازد. در همان زمان، او یک معادله عامّی از حرکت را یافت، که آن نیز به شیوه‌ی ریمانی با هندسه مشخص می‌شد.

شعار او؛ فیزیک به صورت هندسه، را بسیاری از جانشینانش ادامه دادند!

آغاز

در سال ۱۹۰۵، به هنگامی که اینشتین در سن بیست و شش سالگی بود، شادمانه در اداره‌ی ثبت اختراع برن کار می‌کرد، با وجود این به منظور برقراری آشنایی بیشتر با فیزیکدانان نظری دیگر، او سه مقاله در سالنامه فیزیک منتشر کرد. این سالنامه مُجلد ۱۷ از مجله بود و چنانکه ماکس بورن اظهار می‎کند؛

این شماره، یکی از برجسته ترین مجلدها در کل ادبیات علمی است. این سالنامه شامل سه مقاله از اینشتین، هر یک درباره موضوع متفاوتی بود، که امروزه هر کدام یک شاهکار به شمار می آید.

نخستین مقاله او در سال ۱۹۰۵ سهمی از نظریه کوانتوم داشت، که با تصور و توصیف باریکه‌های نور به صورت بارش‌هایی از ذرات یا کوانتوم‌ها، نظريه‌ی اثر فوتوالکتریک را شکوفا کرد.(برای مطالعه‌ی کامل اثر فوتوالکتریک بهقسمت سوم رجوع کنید)

مقاله‌ی دوم، درباره‌ی واقعیت مولکول‌های مشاهده پذیر به صورت ذرات کلوئیدی بود.

توجه این بخش از بحث ما، بر روی سومین مقاله است، که در واقع برداشت اینشتین از نظریه نسبیت را شرح می‌دهد.

هنگامی که اینشتین وارد این میدان شد، نظریه‌ی نسبیت، تاریخی طویل و برجسته‌ای داشت. اینشتین در زمره‌ی پیشگامانی که بعضی از آن‌ها، غول‌هایی همچون گالیله، نیوتون، ماکسول و لورنتس بودند، محسوب می‌شود.

گالیله می‌گوید، اصل نسبیت برای علم مکانیک در شیوه معمولی او که آشکارا مشاهده پذیر است، به کار می‌آید؛

با دوست خود در کابین زیر عرشه‌ی کشتی بزرگی بروید و تعدادی مگس، پروانه و جانداران پرنده دیگر همراه خود ببرید. کاسه‌ی بزرگی محتوی آب که چند ماهی در آن باشد فراهم کنید؛ بطری محتوی آبی را در جایی آویزان کنید، به طوری که آب درون آن قطره قطره روی ظرف پهنی که زیر آن باشد، بریزد. در کابین را ببندید. وقتی کشتی آرام و بی حرکت است، به دقت مشاهده کنید که چگونه پرندگان کوچک با سرعت‌های مساوی به همه اطراف کابین پرواز می‌کنند، اما ماهی بی تفاوت در همه جهات شنا می‌کند؛ قطره‌ی آب در ظرف زیر آن می‌افتد و در پرتاب چیزی به طرف دوست خود، لازم نیست قوت پرتاب شما در یک جهت بیشتر از جهت دیگر باشد. البته در صورتی که فاصله‌ها مساوی باشند. با پاهای خود به طور هماهنگ به بالا بجهيد، در هر جهت از فضاهای مساوی می‌گذرید. وقتی همه این موارد را به دقت مشاهده کردید (گرچه شکی نیست که وقتی کشتی آرام و بی حرکت است هر چیزی می‌باید به همین طریق صورت گیرد) اگر کشتی با هر سرعتی که شما می‌خواهید پیش برود، مادامی که حرکت یکنواخت است، افت و خیزی ندارد و شتاب نمی‌گیرد، در می‌یابید که در تمام موارد مذکور کمترین تغییری حاصل نمی‌شود، به طوری که در هر یک از آن موارد نمی‌توانید بگویید کشتی در حال حرکت است یا در حال سکون!

کشتی گالیله، یا هر سیستم دیگری که با سرعت ثابت حرکت می‌کند، در واژگان جدید یک چارچوب مرجع لخت اینرشیال، یا فقط چارچوب تخت نامیده می‌شود، زیرا در آن قانون لختی گالیله محفوظ می‌ماند. تعمیم اصل نسبیت گالیله به ما می‌گوید، که قانون‌های مکانیک در هر چارچوب لختی دقیقا یکسان است. (شما نمی‌توانید از هر یک از آثار مشاهده شده در کشتی، بگویید که کشتی در حال حرکت است یا در حال سکون)

گزاره اصل نسبیت نیوتون، که او از سه قانون حرکتش استخراج کرد، بیان مشابهی بود، به جز آن که موضوع بحث انگیز فضای ساکن را مطرح می‌کرد؛ حرکت‌های اجسامی که در فضای معینی گنجیده‌اند، در میان خودشان به یک منوال است، خواه آن فضا در حال سکون باشد، یا به طور یکنواخت حرکت کند، به جلو در یک خط مستقیم، بدون هرگونه حرکت دورانی.

 اما این پرسش پیش می‌آید که در حال سکون را نسبت به چه چیزی تعریف می‌کنیم؟

نیوتون به مفهوم فضای مطلق باور داشت، فضای مطلقی که هرگونه حرکت یا فقدان حرکتی را می‌توان به آن ارجاع کرد. او به همین منوال یک چارچوب زمان مطلق را اتخاذ کرد، که در آن اندازه‌گیری هرگونه حرکتی امکان پذیر می‌شد؛ یک چارچوب زمان برای همه ناظران به کار می آید.

ماکسول و معاصران او مفهوم فضای مطلق نیوتون را پذیرفتند و آن را با ملأ فراگیری به نام اِتِر پر کردند. نقش اصلی اِتِر برای نظریه پردازان قرن نوزدهم این بود، که قطع نظر از فضای خالی مکانیسمی برای انتشار نور و میدان‌های مغناطیسی دیگر فراهم آورد.

معلوم شده بود که اِتِر ابزار نظریه‌ای چندکاره است. نظریه‌پردازان بریتانیا و دیگر کشورهای اروپایی هرگز نتوانستند به این اجماع نظر برسند، که کدام یک از مدل‌های متعدد مطرح شده برای اِتِر ، یک مدل استاندارد است.

کسی که فیزیک اِتِر و ارتباط‌های آن را با نظریه‌ی میدان با وضوح بسیار می دانست و در عین حال به اینشتین یاری رساند تا راه خود را بیابد، هندریک نورت بود؛ او از سال‌های ۱۸۷۷ تا ۱۹۱۲ استاد فیزیک نظریی در دانشگاه لیدن بود، نسل‌های مختلف از فیزیکدانان جوان توانایی فوق‌العاده او برای ایفای نقش دوگانه‌ای را که به عنوان نظریه پرداز خلاق و منتقد مشفق داشت، می ستودند. شیوه‌ی کار او مانند ماکسول و گیبس جمع آوری مکتبی از دانشجویان محقق نبود، با این وجود فیزیکدانانی از سراسر جهان در جلسات سخنرانی‌هایی که درباره‌ی الكترودینامیک داشت، حضور می‌یافتند. در ابتدای قرن همگی او را به عنوان رهبر جامعه بین المللی فیزیک می‌شناختند. در آغاز سال ۱۹۱۱، لورنتس به عنوان رئیس کنفرانس‌های سلوی در بروکسل عمل میکرد. ارنست سلوی یک شیمیدان صنعتی با ثروت فوق العاده بود و علاقه‌ای غیرحرفه‌ای به فیزیک داشت. او صورت حساب هزینه مکان و پذیرایی شایسته شرکت کنندگان کنفرانس را می‌پرداخت. لورنتس تنها کسی بود، که می‌توانست میان این جمعیت بین المللی که اینشتین، آن‌ها‌ را ساحره‌های یکشنبه ها می‌نامید، هماهنگی ایجاد کند. یکی از زندگینامه نویسان لورنتس، راسل مک کورمکمی‌نویسد؛

 اظهارنظر دیگران در باره‌ی لورنتس خبر از، دانش بی همتای او، حسن تدبیر، توانایی تلخیص بغرنج‌ترین مباحث و استدلال‌هایی به طور واضح و مهم‌تر از همه، مهارت زبان شناختی بی رقیب او می‌داد.

 اینشتین پس از نخستین حضور در کنفرانس سلوی، به یکی از دوستانش نوشت:

لورنتس اعجوبه ای از تیزهوشی، ذکاوت و تدبیر استادانه است. او یک اثر هنری زنده است. به عقيده من او هوشمندترین نظریه پرداز عصر حاضر است!

هدف اصلی لورنتس، به عنوان یک نظریه پرداز، ایجاد وحدت فیزیک ماده در سطح مولکولی با فیزیک میدان‌های الکترومغناطیسی ماکسول بود. یکی از مبانی نظريه‌ی لورنتس این مفهوم بود، که جایگاه میدان‌های الکتریکی و مغناطیسی یک اِتِر مطلقا ساکن است، که بدون مقاومت قابل اندازه‌گیری در کل ماده نفوذ می‌کند، سنگ بنای دیگر با این فرض فراهم آمد، که ماده مرکب از ذرات باردار بسیار کوچکی است و لورنتس سرانجام تشخیص داد، آن‌ها همان ذراتی به نام الکترو‌‌ن‌ها هستند، که ج.ج. تامسن در سال ۱۸۹۷ در پرتوهای کاتودی کشف کرده است. الکترون‌ها میدان‌های الکتریکی و مغناطیسی تولید می‌کنند و این میدان‌ها به نوبه‌ی خود، راهنمای الکترو‌ن‌ها در اِتِر ساکن می‌شوند. لورنتس معادلات ماکسول را برای چارچوب مرجع اِتِر ساکن نوشت تا میدان‌ها را توصیف کند و پیام این معادلات را پذیرفت که در آن چارچوب، سرعت نور صرف نظر از سرعت و جهت منبع نور همواره یکسان است.

برای تلخیص و نقل داستان پیرامون نقطه نظر اینشتین، دو ناظر را تصور کنید که یکی در اِتِر ساکن است و دیگری در اتاقی ساکن است، که با سرعت ثابتی نسبت به اِتِر حرکت می‌کند. این اتاق حامل یک منبع نور ثابت است و دو ناظر اثرات پیام‌های نوری تولید شده از منبع را مقایسه می‌کنند. برطبق نظریه‌ی لورنتس، ناظر اول متوجه می‌شود، که سرعت یک باریکه‌ی نور مستقل از جهت آن است. اما ناظر دوم چنین چیزی را متفاوت می‌بیند؛ فرض کنید یکی از دیوارهای اتاق او از باریکه‌ی نور، پس از تولید شدن، دور می شود، در حالی که دیوار مقابل به طرف باریکه‌ی نور نزدیک می‌شود. اگر منبع نور در مرکز اتاق ثابت باشد، باریکه‌ی نور گسیل یافته به طرف دیواره‌ای که از باریکه‌ی نور پَس کشیده می‌شود کُندتر از باریکه نوری به نظر می‌رسد که به طرف دیواره دیگر گسیل می‌یابد، دیواره‌ای که به باریکه نزدیک می شود. بنابراین برای ناظر دوم سرعت نور در همه جهات یکسان نخواهد بود.

برای اینکه این بحث را به ماورای یک آزمایش ببریم، می توانیم زمین را به منزله‌ی یک اتاق تصور کنیم که در اِتِر حرکت می‌کند و نتیجه‌گیری کنیم که برای ما، یعنی ساکنان اتاق، سرعت نور باید به هنگامی که نور در جهات گوناگون منتشر می شود، متفاوت باشد. در اواخر قرن نوزدهم چند آزمایش برای این انگیزه، طراحی و اجرا شد. ظریف‌ترین این آزمایش‌ها را آلبرت مایکلسون و ادوارد مورلی، در سال ۱۸۸۷ به انجام رساندند. نتیجه‌گیری آن‌ها، احتمالا مشهورترین نتیجه منفی در تاریخ فیزیک، این بود که سرعت نور در فضای خالی اصلا به حرکت، جهت، یا محل منبع نور بستگی ندارد!

این امر ضربه زبان آوری برای نظريه‌ی الكترونی لورنتس بود، اما کاملا مهلک نبود. او دریافت که می‌تواند نتیجه گیری مایکلسون- مورلی را با این فرض توضیح دهد که اشیای مادی در جهت حرکتشان اندکی منقبض می‌شوند و فقط همین کافی است تا آزمایش مایکلسون- مورلی و تلاش‌های دیگر، برای مشخص کردن حرکت زمین در اِتِر به وسیله تغییرات اندازه‌گیری در سرعت نور را عقيم سازد. به نظر لورنتس این انقباض، تغییر بسیار جزئی نیروهای مولکولی در جهت حرکت بود.

اکنون وقت آن است که اینشتین، یک اندیشمند درجه یک را به میدان بیاوریم و بررسی آفرینش آنچه را که با نامنظریه‌ی نسبیت خاص به ذهن او رسیده بود، دنبال کنیم. او با اصل نسبیت گالیله آشنا شد، از مفهوم فضا و زمان مطلق نیوتون آگاهی یافت. آثار لورنتس را با دقت تمام خواند و تحت تأثیر این امر قرار گرفت که آزمایشگران نمی‌توانند به وسیله اندازه‌گیری تغییرات در سرعت نور، راهی برای تشخیص حرکت زمین نسبت به اِتِر بیابند.

(پس از پایان بحث نسبیت، گریزی به بحث پرتوهای کاتدی و اشعه‌ ایکس و الکترون‌ها و مطالب مرتبط با آن خواهیم زد، اما اکنون به ادامه‌ی این بحث جذاب و شیرین خواهیم پرداخت)

مکتب فضا-زمان

دو نوع نظریه‌ی مهم برای اینشتین وجود داشت. او می نویسد:

آن‌ها اکثرا سازنده‌اند و می‌کوشند تا با شروع از مطالب نسبتا ساده و بررسی آن‌ها، تصویری از پدیده‌های پیچیده تر بسازند.

 او به عنوان مثال نظريه‌ی مولکولی گازها را ذکر می‌کند. این نظریه با فرضیه‌ی حرکت مولکولی آغاز می‌شود و از آن توجیهی برای تنوع وسیعی از خواص مکانیکی، گرمایی و پخشندگی گازها ساخته می‌شود. اینشتین ادامه می‌دهد که؛ وقتی ما می‌گوییم در فهمیدن گروهی از فرایندهای طبیعی موفق بوده‌ایم، همواره منظورمان این است که یک نظریه سازنده یافت شده است که فرایندهای مورد بحث را در بر می‌گیرد.

از گالیله و نیوتون به بعد نظریه‌پردازان نیز آنچه را که اینشتین نظریه‌های اصلی می نامد، آفریده‌اند. این‌ها نظریه‌هایی هستند که؛ روش‌های تحلیلی را به کار می‌گیرند نه روش‌های ترکیبی (سنتزی). عناصری که اساس و نقطه شروع آن‌ها را تشکیل می‌دهند، به طور فرضی ساخته نشده‌اند، بلکه آن‌ها به طور تجربی کشف شده‌اند، ویژگی‌های عمومی فرایندهای طبیعی را دارند، اصولی که به ضوابط فرمول‌بندی شده ریاضیاتی آن‌ها رونق می‌بخشد، ضوابطی که فرایندهای جداگانه یا بازنمایی‌های نظریه‌ای آن‌ها را ارضا می‌کند.

 اینشتین برای ارائه نمونه عالی یک نظریه‌ی اصلی به علم ترمودینامیک اشاره می‌کند، که بر اصول انرژی و آنتروپی بنا شده است و امروزه قانون‌های اول و دوم ترمودینامیک نامیده می‌شوند.

اینشتین نسبیت را به چشم یک نظریه اصلی می‌نگریست. او مقاله‌ی سال ۱۹۰۵ خود، درباره نسبیت را با مسلم دانستن دو اصل تجربی آغاز کرد، دو اصلی که نظریه‌اش، با همه‌ی استنتاجات شگفت‌انگیزش، بر پایه‌ی آن‌ها قرار گرفته است. اصل نخست، اصل نسبیت تعمیم یافته‌ی گالیله بود، با این بیان که؛ (آن طور که اینشتین چند سال بعد آن را مطرح کرد)

قانون‌های طبیعت مستقل از حالت حرکت چارچوب مرجع است،

 مادامی که این چارچوب بدون شتاب باشد(چارچوب لخت باشد).

عبارت قانون‌های طبیعت همه چیز را شامل می‌شود منشأ قانون‌های الکتریکی، اپتیکی و مکانیکی را در بر می‌گیرد. این اصل دموکراتیک باشکوهی است که؛ همه چارچوب‌های مرجع لخت برابرند، هیچ تفاوت و ارجحیتی وجود ندارد!

اصل دوم اینشتین بازشناسی رسمی ثابت بودن نور را ارائه می‌دهد:

نور در فضای خالی همواره با سرعت معینی منتشر می‌شود و این امر مستقل از حالت حرکت جسم گسیلنده است.

در حالی که لورنتس برای توضیح تغییر ناپذیری سرعت نور با یک نظریه‌ی سازنده، در کشمکش با نظریه‌ای بود که، حرکت نور را وابسته به نیروهای مولکولی فرض می‌کرد، اینشتین تمام این پیچیدگی‌ها را کنار گذاشت و به سادگی ثابت بودن سرعت نور را به صورت یک اصل مسلم ارتقا بخشید. برای لورنتس و معاصران او این امر یک مسئله و چالش حل نشدنی و برای آلبرت اینشتین آلمانی یک اصل بود!

دو اصل اینشتین او را به این نتیجه گیری هدایت کرد، که سرعت نور در فضای آزاد تنها اندازه‌ی فضا و زمان است که به طور موثقی از یک ناظر به ناظر دیگر ثابت است. همه‌ی چیزهای دیگر نسبی است. ناظران متفاوت نمی‌توانند قانون‌های فیزیکی خود را در یک چارچوب مرجع مطلق مشترک، آنچنان که نیوتون تعلیم می‌داد، بیان کنند. ناظران در چارچوب‌های لخت متفاوت به اینکه دنیاهای فیزیکی‌شان، بنابر مکتب فضا و زمان متفاوت است، پی می‌برند. این همان چیزی است که اینشتین مطرح می‌کند.

طرح کلی در فضا-زمان، ادغام فضا و زمان با یکدیگر و در نتیجه ایجاد یک محیط یکپارچه با دستگاه مختصاتی یکتا است. برای این کار به سه بُعد مکانی معمول(طول، عرض، ارتفاع) و یک بُعد زمان نیاز داریم؛ این بُعدها مؤلفه‌های مستقل لازم برای مشخص کردن یک نقطه‌ی خاص در یک فضای تعریف شده‌اند. مثلاً در محیط کره‌ی زمین طول و عرض جغرافیایی دو مؤلفه‌ی مستقل دستگاه مختصات‌اند که تنها به‌وسیله‌ی هر دوی آن‌ها باهم می‌توان موقعیت یک نقطه‌ی خاص را تعیین کرد؛ حال در فضا-زمان، شبکه مختصاتی ۱+۳ بُعد را پوشش می‌دهد و چون زمان به عنوان مؤلفه‌ی جدید اضافه شده‌ است، در نتیجه دستگاه مختصات نه تنها می‌تواند نقاط را در محیط مکان‌یابی کند، بلکه می‌تواند رویدادها را نیز تعیین موقعیت نماید. به این ترتیب این دستگاه مختصات می‌تواند تعیین کند که کِی و کجا یک رویداد اتفاق افتاده است. در فضا زمان نمی‌توانیم محور زمان را به صورت جداگانه نشان دهیم، اگر بخواهیم محور زمان را در دستگاه مختصات نشان بدهیم، ناگزیریم که محور زمانی و مکانی را هر دو باهم، و در یک دستگاه مختصات قرار دهیم و این به دلیل ماهیت یکپارچه‌ی فضا-زمان و آزادی در انتخاب دستگاه مختصات است. برخلاف دستگاه مختصات فضایی معمولی، محدودیت‌هایی برای چگونگی اندازه‌گیری‌های مکانی و زمانی وجود دارد؛ این محدودیت‌ها به مدل ریاضی خاص آن و تفاوت‌هایش با ریاضیات و هندسه‌ی اقلیدسی باز می‌گردد.

تا آغاز قرن بیستم گذر زمان مستقل از حرکت در نظر گرفته می‌شد و فرض این بود که در تمام دستگاه‌های مختصات، زمان تنها در یک محور مشخص با سرعت ثابت پیش می‌رود؛ اما تجربیات بعدی نشان داد که زمان در سرعت‌های بالا کندتر حرکت می‌کند (کاهش سرعت زمان با عنوان تأخیر زمان در نسبیت خاص توضیح داده شده‌است)؛ برای مثال یک ساعت اتمی را بر روی یک شاتل فضایی نصب کردند و دیدند که زمان برای ساعت روی شاتل کندتر از زمان در سطح زمین می‌گذرد.

عبارت فضا-زمان به عنوان یک مفهوم عمومی فراتر از رویدادهای فضا-زمان در ۱+۳ بُعد معمولی در نظر گرفته می‌شود، فضا-زمان واقعاً ترکیبی از مکان و زمان است، اما برخی دیگر پیشنهاد کرده‌اند که بُعدهای جدیدی که بعدها اضافه می‌شود هم در مجموعه‌ی تئوری فضا-زمان قرار گیرد (نظریه‌های دیگری وجود دارند که توانسته‌اند بُعدهای جدیدی را اضافه کنند که این بُعدها دیگر شامل مکان و زمان نمی‌شوند)؛ اینکه واقعاً چند بُعد برای توصیف جهان لازم است سؤالی است که هنوز پاسخ قطعی برای آن پیدا نشده‌است. تئوری‌هایی مانند تئوری ریسمان پیش‌بینی می‌کند، که ۱۰ تا ۲۶ بُعد جدید را بتوان اضافه کرد، یا تئوری-اِم داشتن ۱۱ بُعد شامل ۱۰ بُعد مکانی و ۱ بُعد زمانی را ممکن می‌داند؛ باید به این نکته توجه داشت که: داشتن بیش از چهار بعد فقط در اندازه‌های زیر اتمی تفاوت ایجاد می‌کند.

اتساع زمان

اتساع زمان یکی از مفاهیم فیزیکی مربوط به نظریه نسبیت خاص آلبرت اینشتین است، که مبنی بر پایه نسبیت این گونه بیان می‌شود که؛ از دید دو ناظر متفاوت گذر زمان بررسی می‌شود. در مثال آزمایشی ساده؛ یکی با دو سرعت نزدیک به سرعت نور و سرعتی کمتر از سرعت نور (به‌طوری‌که دو بردار سرعت با هم زاویه غیر از ۱۸۰ و صفر درجه بسازند، برای احساس بهتر پدیده اتساع) فرض می‌شود و ناظر دوم ساکن فرض می‌شود.

با انجام یک مجموعه عملیات ریاضی در نهایت فرمول‌های محاسبه اتساع زمان در نسبیت خاص به شرح زیر است:

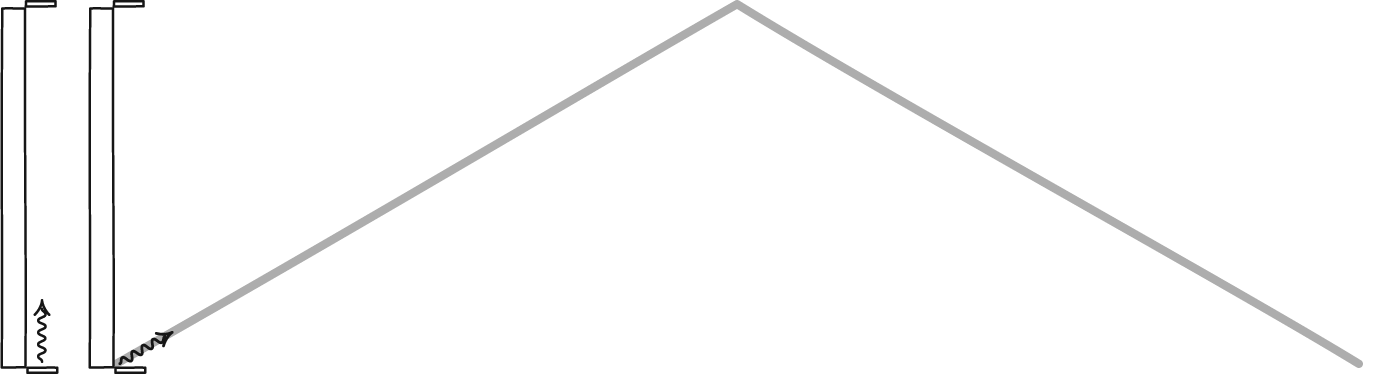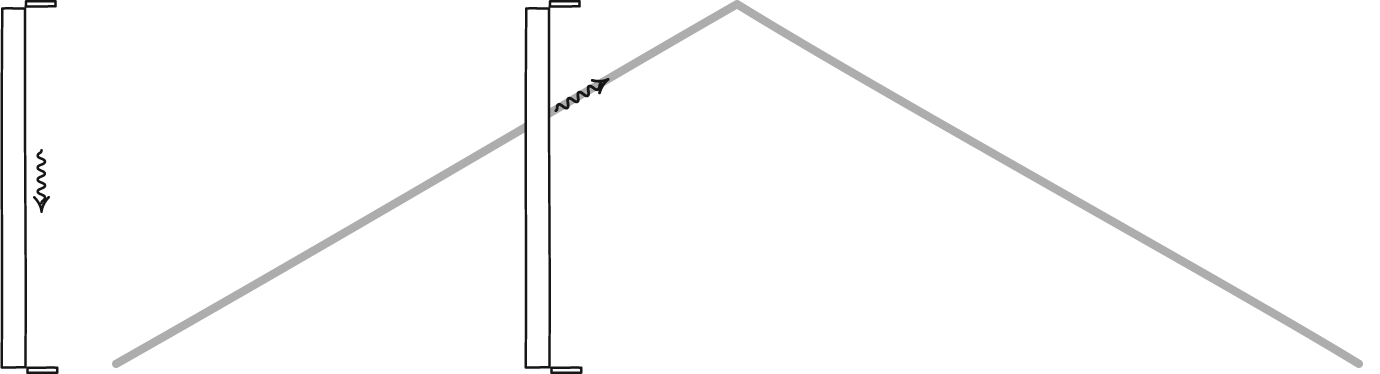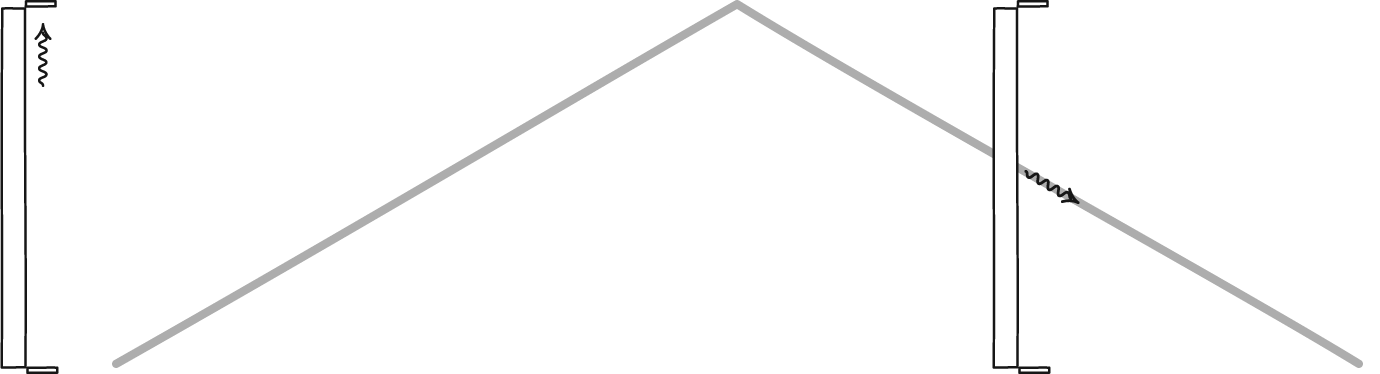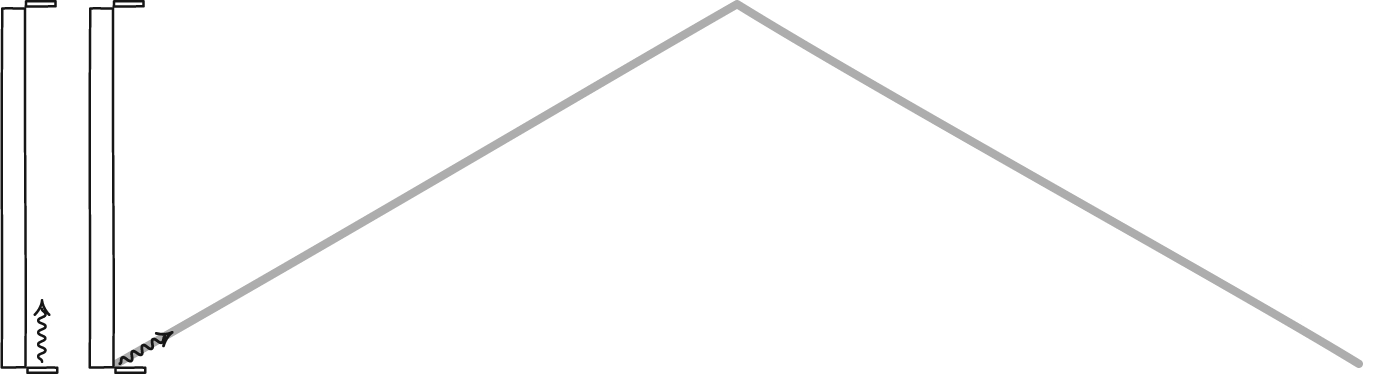
به طور کلی می‌توان گفت، ساعت در حال سکون زمان بیشتری را اندازه‌گیری می‌کند، به طور مثال اگر شخصی با سرعت ۰.۹۹ سرعت نور به مدت یک سال در حرکت باشد، این زمان معادل با ۷ سال زمان گذشته در زمین است. در زندگی عادی، جایی که با سرعتی بسیار اندک نسبت به سرعت نور حرکت می‌شود نمی‌توان اتساع زمان را مشاهده کرد اما در سرعت‌های بالا (نزدیک به سرعت نور) پدیده اتساع زمان را می‌شود یافت. با این وجود یکی از کاربردهای این پدیده در ساعت ماهواره‌های GPS است که آن‌ها را دقیق می‌کند. بدون اطلاع از اتساع زمان GPS بی‌ارزش بود.

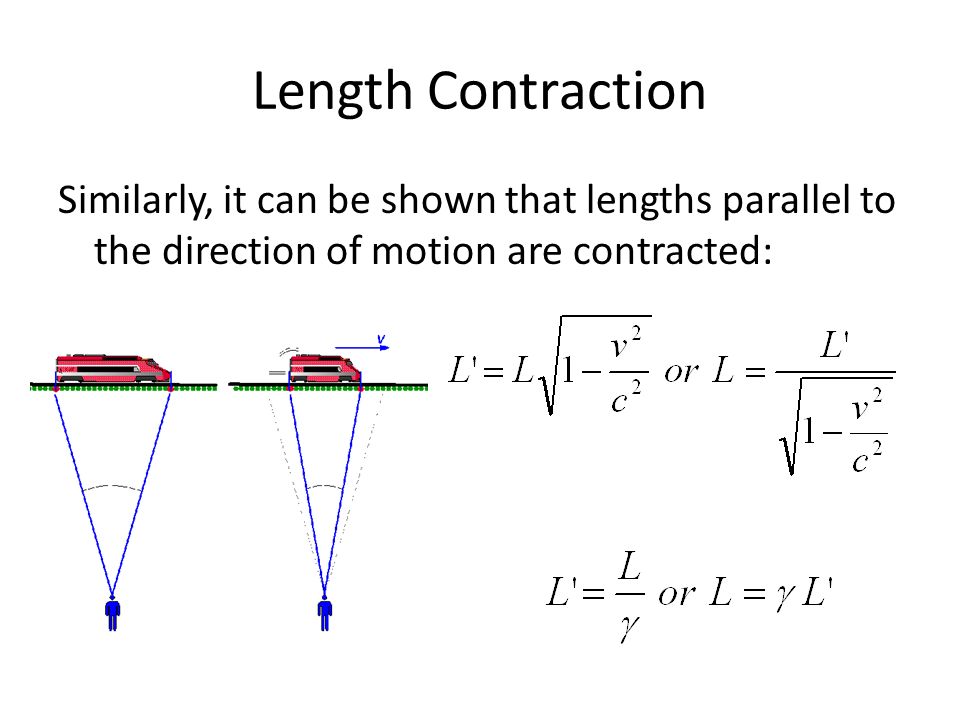
انقباض طول

انقباض طول که به انقباض لورنتس–جرالد نیز معروف است، یکی از نتایج نظریه‌ی نسبیت خاص است که آلبرت اینیشتین در سال ۱۹۰۵ ارائه داده بود.

مطابق این نتیجه، در تمام اجسامی که با سرعتی غیر از صفر نسبت به یک ناظر در حال حرکت هستند، طول کاهش می‌یابد. نکته مهم این است که این تغییر طول در سرعت‌های پایین بسیار ناچیز و قابل چشم پوشی است و تنها در مواردی محسوس است که سرعت جسمی حداقل یک دهم سرعت نور باشد.

هم‌ارزی جرم و انرژی

معادله های اتساع زمان و انقباض طول، بیان کننده نسبیت زمان و طول است که آموزه‌ی جدید فضا و زمان اینشتین را مجسم می‌کند، این معادله‌ها آنچه را که فیزیکدانان،  سینماتیک یعنی فیزیک بدون مفهوم انرژی می‌نامند، در بر میگیرد. گام بعدی اینشتین توسعه نظریه‌اش در علم دینامیک بود که انرژی را نیز شامل می‌شد. او در مقاله درخشان دیگر سال ۱۹۰۵ خود، ساختن علم دینامیکی را آغاز کرد که به نتیجه بسیار جالبی انجامید: جرم یک جسم اندازه‌ای از محتوای انرژی آن است.

 این قضیه به مدت چند سال مشغله فکری او بود. در سال ۱۹۰۶، این فکر به ذهن او خطور کرد که، پایستگی جرم حالت خاصی از قانون پایستگی انرژی است. یک سال بعد او به این نتیجه رسید که، با توجه به لختی (اینرسی)، جرم m، هم ارز با محتوای انرژی، به بزرگی mc2 است. این مطلب بیان کلامی معادله‌ای است که امروزه شهرت جهانی دارد یعنی؛

زیر بنای این معادله‌ی انرژی، این مفهوم است که جرم، مانند زمان و طول، نسبی است. زمان و طول هر دو، به سرعت نسبی جسم مشاهده شده بستگی دارند و بنابراین در مورد جرم هم چنین است.

در این فرمول E به معنای انرژی یک سامانه فیزیکی، m جرم سیستم و c سرعت نور در خلاء است.

از آنجا که سرعت نور در مقایسه با واحدهای روزمره عدد بسیار بزرگی است، این فرمول نشان می‌دهد که هر مقدار کوچکی از ماده حاوی مقدار بسیار زیادی از انرژی است. مقداری از این انرژی ممکن است به صورت نور و گرما توسط فرایندهای شیمیایی یا هسته‌ای آزاد شود. همچنین این فرمول بیان می‌کند، که یکاهایی از جرم به یکاهایی از انرژی (بدون توجه به اینکه کدام یک از سامانه‌های اندازه‌گیری به کار رود) تبدیل می‌شود.

هم‌ارزی جرم و انرژی در اصل به عنوان یک پارادوکس در نسبیت خاص بوده که توسط آنری پوانکاره شرح داده شده و اینشتین آن را در سال ۱۹۰۵ در مقاله‌ی آیا اینرسی یک جسم به انرژی درونش بستگی دارد؟ ارائه کرده‌است. اینشتین اولین کسی بود که پیشنهاد داد هم‌ ارزی جرم و انرژی یک اصل کلی باشد و آن را نتیجه‌ای از تقارن فضا-زمان می‌دانست.

یکی از نتایج هم‌ارزی جرم و انرژی این است، که اگر یک جسم ایستا (بی‌تغییر) باشد، باز هم مقداری انرژی درونی یا داخلی دارد که به آن انرژی نامتغیر یا انرژی سکون گفته می‌شود. جرم سکون و انرژی سکون هم‌ ارزند و با یکدیگر متناسب می‌مانند. وقتی جسمی در حال حرکت (نسبت به یک ناظر) است، مقدار کل انرژی‌اش از انرژی سکون بیشتر می‌باشد. جرم سکون (یا انرژی سکون) یک مقدار خاص در این مورد است، زیرا بدون در نظر گرفتن آن، حرکت ثابت باقی می‌ماند، حتی در سرعت‌های شدید یا گرانشِ در نظر گرفته شده در نسبیت خاص و عام؛ بنابراین آن را جرم ثابت نیز می‌نامند.

باید توجه شود که در نظریه نسبیت عام، جرم لختی و جرم گرانشی با هم برابر هستند، بنابراین این فرمول‌بندی برای جرم گرانشی نیز صادق است. همان‌طور که گفته شد، در اینجا m، جرم جسم در حال سکون است. اما اگر این جسم با سرعت v در حال حرکت باشد آنگاه داریم:

حال اگر سرعت این جسم بسیار کمتر از سرعت نور باشد (  ) آنگاه از معادله بالا به راحتی به دست می‌آوریم:

که نشان می‌دهد، انرژی یک جسم متحرک با سرعت بسیار پایین (که در زندگی روزمره با آن‌ها سر و کار داریم) به اندازه (  ) بیشتر می‌شود؛ که این مقدار برای ما آشنا است و همان انرژی جنبشی است، که در مکانیک کلاسیک با آن سر و کار داریم.

پس از آنکه قانون پایستگی جرم و انرژی در کنش‌های هسته‌ای نقض شد، توسعه‌ی پایستگی جرم-انرژی سبب عدم ابطال قانون پایستگی گشت. این معادله گاه برای توضیح پدیده‌های فیزیک هسته‌ای مثلاً در واپاشی هسته‌ای به کار می‌رود.

برای فهم بهتر این موضوع یک مثال معروف را مطرح می‌کنیم.

واکنش تشکیل هیدروژن را در نظر بگیرید:

 (H2(g) + O2(g) → 2 H2O(l) + 572 kJ (286 kJ/mol

در تشکیل یک کیلوگرم (H2O) در حدود  1/5‌ × 10(1/10) کیلوگرم جرم به انرژی تبدیل می‌شود. واکنش‌های هسته‌ای مؤثرترند، آن‌ها چند دهم از یک درصد جرمی را که وارد واکنش می‌شود به انرژی تبدیل می‌کنند. وقتی ماده با پادماده برخورد می‌کند، تبدیل کامل است. اینشتین در مقاله‌ی ۱۹۰۵ خود اظهارنظر کرد که مواد رادیواکتیو، مانند رادیم، در جریان واپاشی مقداری جرم قابل اندازه‌گیری از دست می‌دهند، اما سال‌های زیادی او نتوانست پیامدهای عملی هم ارز جرم - انرژی را ببیند. (در سال ۱۹۳۴، روزنامه پیتزبرگ گازت داستان یک سخنرانی اینشتین را با تیتر درشت چنین گزارش کرد: اینشتین امید انرژی اتمی را خاردار کرد. تلاش‌های آزاد شدن نیروی عظیم بی ثمری نامیده می‌شود.) درس کامل (هم ارزی انرژی و جرم) در سال‌های ۱۹۴۰ و ۱۹۴۵ با ظهور فیزیک هسته‌ای، سلاح‌های هسته‌ای، راکتورهای هسته‌ای و اضطراب هسته‌ای، آموخته می‌شد.

توفیق بیشتری از نظریه‌ی نسبیت این بود، که نقطه پایان ابدی بر مفهوم اِتِر گذاشت، تنها به این وسیله که برای وجود اِتِر، هیچگونه دلیل موجهی باقی نگذاشت. اگر اِتِری وجود می‌داشت، یک چارچوب مرجع مطلق و برتری، مخالف با اصل اول اینشتین فراهم می آورد و اگر حرکت در اِتِر با تغییراتی در سرعت نور آشکار می‌شد، اصل دوم او را نقض می‌کرد. آگهی درگذشت اِتِر را که اینشتین و لئوپولد اینفلد در کتاب ارزنده‌ای برای خواننده‌ی عام با عنوان تکامل فیزیک، چنین می خوانیم:

اتر نه ساختار مکانیکی و نه حرکت مطلقش را آشکار می‌کند. چیزی از خواص آن باقی نمی‌ماند، مگر آنکه برای منظوری اختراع شده باشد، یعنی توانایی‌اش برای انتقال امواج الکترومغناطیسی.

فیزیک در حکم هندسه

نظریه‌ی ۱۹۰۵ اینشتین در طرح‌هایش گزاره توانمندی درباره‌ی جهان فیزیکی ایجاد کرده بود، اما اینشتین بلافاصله دانست که جا برای اصلاح آن وجود دارد. از یک سو به نظر می‌رسید که این نظریه به سیستم‌های لخت محدود باشد. از سوی دیگر با نظريه‌ی الكترومغناطیسی ماکسول سازگار بود اما با نظریه‌ی بزرگ دیگر که اینشتین به ارث برده بود، یعنی نظریه گرانش نیوتون سازگاری نداشت. برای تحقق یافتن پتانسیل آن، نظریه باید سیستم‌های غیر لخت (non inertial) یعنی سیستم‌هایی را که نسبت به یکدیگر شتاب می‌گیرند، بازشناسی کند و در عین حال حوزه‌اش را تا گرانش گسترش دهد.

نخستین مرحله‌ای که اینشتین در این راه پیمود، با یک تیر دو نشان زد. چنان که او بعدا شرح داد:

 من در اداره ثبت اختراعات در برن روی یک صندلی نشسته بودم، ناگهان فکری به خاطرم خطور کرد؛ اگر شخصی به طور آزاد سقوط کند، وزن خودش را احساس نخواهد کرد. من بهت زده شده بودم. این فکر ساده، تأثیر عمیقی بر من داشت و مرا به سوی نظریه‌ای از گرانش سوق داد.

این نخستین تصویر ذهنی اینشتین بود، از آنچه بعدا او آن را اصل هم ارزی نامید. ایده اصلی این است که گرانش امری نسبی است. مثلا شخصی که درون یک آسانسور در بسته‌ی در حال سقوط، به آزادی ساقط می‌شود، متوجه هیچ گونه شاهدی از گرانش نمی‌شود؛ همه چیز در آسانسور بدون وزن و در حال سکون به نظر می‌رسد. از سوی دیگر، ناظر بیرونی، آسانسور را در حال شتاب چسبیده به یک میدان گرانشی می‌بیند.

ساکنان آسانسور تجربه مخالفی دارند، هرگاه آسانسور از میدان گرانشی جدا شود و به وسیله طناب پیوسته به آسانسور، با آهنگ ثابتی به سوی بالا شتاب گیرد. در این حال ناظر بیرونی متوجه میدان گرانشی نمی شود، در حالی که ناظر درونی و همه متعلقات او چنان به کف آسانسور ثابت نگه داشته می‌شوند، که گویی آنان دقیقا در یک میدان گرانشی‌اند.

در اینجا هم ارزی بین یک سیستم شتابدار در فضای بدون میدان و یک سیستم لخت در میدان گرانشی است. اینشتین با این طریق استدلال به آغاز این ادراک رسید، که چگونه می‌توان هم گرانش و هم شتاب را در نظریه نسبیت مطرح کرد.

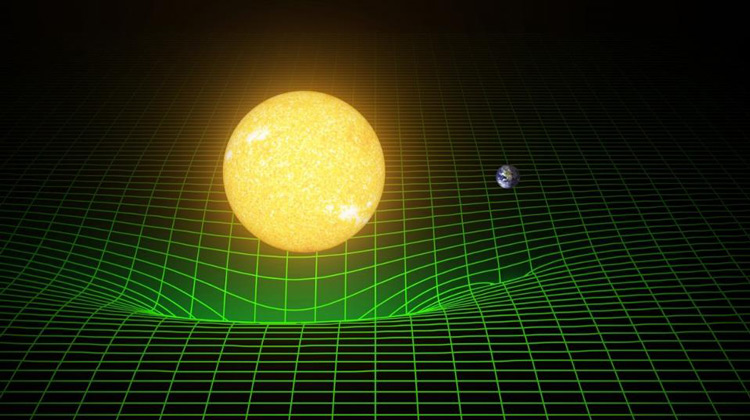
تصویر آسانسور بر یک طناب (که بعدها به وسیله اینشتین و اینفلد توسعه یافت) نشان می‌دهد، که چگونه اصل هم ارزی شکل اولیه‌ی پیشگویی اینشتین درباره خَمِش پرتوهای نور بر اثر گرانش را، که ده سال بعد جنجال جهانی را برای او به بار آورد، توجیه می کرد. آسانسوری بر یک طناب را با پرتو نوری تصور کنید که در عرض آسانسور از چپ به راست سیر می کند. ناظر بیرونی آسانسور و پرتو نور را آن طور که در شکل زیر نشان داده شده است، می بیند. چون پرتو نور زمان معینی برای سیر از یک دیواره به دیواره دیگر می‌گیرد و آسانسور در طی آن زمان با شتاب بالا می‌رود، ناظر بیرونی مسیر پرتو نور را آن طور که نشان داده شده است، اندکی خمیده می‌بیند. ناظر درونی نیز پرتو نور را خمیده می‌بیند، اما آگاهی از شتاب ندارد و این اثر را به میدان گرانشی هم ارز آن که ناظر را به کف آسانسور نگه داشته است، نسبت می‌دهد. ناظر درونی باور دارد، که پرتو نور می‌باید به میدان گرانشی واکنش نشان دهد زیرا میدان انرژی دارد و بنابراین، با تجویز (فرمول هم ارزی) جرم نیز دارد. از این رو پرتو نور مانند هر جسم جرم دار دیگر، به یک میدان گرانشی واکنش نشان می‌دهد.

اینشتین با اصل هم ارزی به عنوان راهنما، در سال ۱۹۰۷ عمومیت دادن نظریه نسبیت اش را به طوری آغاز کرد که گرانش و شتاب را در بر گیرد. همچنان که او پیش می‌رفت، به طور فزاینده‌ای متقاعد می شد که با مسئله‌ای در نوع عجیبی از هندسه سروکار دارد. حتی در نسبیت خاص نشانه هایی وجود دارد که شتاب و گرانش هم ارز، تخطّی‌هایی از بعضی قضیه‌های اقلیدسی تشکیل می‌دهند، قضیه‌هایی مانند این قاعده که نسبت محیط دایره به قطر آن برابر با عدد (عدد π) است. مثلا اینشتین توانست با استفاده از نسبیت خاص استدلال کند، که نسبت اندازه‌گیری شده‌ی محیط به قطر برای دیسکی که به سرعت می‌چرخد، باید اندکی بزرگتر از (عدد π) باشد.

در سال ۱۹۱۲، وقتی که اینشتین از پراگ به زوریخ بازگشت، امیدوار بود راه نجات را در ریاضیات از هندسه‌ی غیراقلیدسی بیابد. او کمک‌های مهمی از دوست ارجمندش مارسل گروسمان استاد ریاضیات در ETH زوریخ، دریافت کرد. او به اینشتین توصیه کرد، که اثر برنهارد ريمان درباره هندسه‌ی دیفرانسیلی را بخواند. در سال‌های ۱۸۵۰، ریمان مطالعه جامعی از فضاهای غیراقلیدسی با مشخص کردن انحنای خطوط کشیده شده در آن فضاها، به عمل آورده بود.

ریمان برای محاسبه‌ی انحناها از ابزاری ریاضی استفاده کرد، که مینکوفسکی شصت سال بعد، آن را به صورت عنصر خط مربع شده (ds2) وام گرفت. دقیقا آن طور که ریاضیدانان می‌خواهند، ریمان شکل عمومی کاملی از معادله‌ی عنصر خط را تصور می‌کرد، شامل هر تعداد بُعد و در برگیرنده‌ی همه جملات مجذور ممکن.

مثلا، هندسه دو بعدی اقلیدسی با عنصر خط را در نظر بگیرید:

ds2= dx2 + dy2

در طرح ریمان، ما این معادله را بسط می‌دهیم، تا شامل جمله‌هایی شود غیر از دو عامل درجه‌ی دوم ممکن از لحاظ ریاضی، یعنی dxdy و dydx

ds2= (1)dx2 + (0)dxdy + (0)dydx + (1)dy2

جملات اضافی در ضرایب صفر ضرب می‌شوند، زیرا آن‌ها واقعا در معادله‌ی ds2 ظاهر نمی‌شوند. دو جمله‌ی دیگر ضریب یک دارند، مانند معادله‌ی اولیه همه‌ی آن چه لازم است، ما درباره‌ی هندسه‌ی اقلیدسی دو بُعدی در آنالیز ریمانی بدانیم، چهار ضریب در پرانتزها در اخرین معادله است. که آن‌ها را به شکل ماتریس g نشان داده و آن راتانسور متریک می‌نامیم.

ماده‌ی خام ریاضیاتی برای محاسبه انحنای ریمانی در تانسور متریک، برای هندسه موردنظر محصور شده است؛ فرض کنید هندسه‌ای با تانسور متریکش مشخص و تعریف شده است، ریمان نشان می‌دهد که چگونه انحنای آن را محاسبه کنیم. سه تانسور متریک به دست آمده، اتفاقا انحنای صفر به دست می‌دهد؛ آن‌ها هندسه‌های تخت را مشخص می‌کنند. اما بسیاری هندسه‌های دیگر انحنا دارند و بنابراین غیراقلیدسی‌اند، به طوری که تانسورهای متریکشان در آنالیز ریمانی آشکار می‌شود.

سرانجام اینشتین در سال ۱۹۱۵ دریافت که با ابزارهای ریاضیاتی ریمانی می‌تواند یک معادله میدان به دست آورد، که گرانش و هندسه را به طور کامل به هم متصل کند. معادله او، تقلیل یافته به ساده ترین شکل آن به صورت زیر است:

که در آن G ثابت گرانشی نیوتونی و  G و T تانسورها هستند، به این معنی که آن‌ها مخصوصا به طوری مشخص شده‌اند که این معادله دقیقا یک شکل ریاضی در همه چارچوب‌های مرجع، چه لخت و چه غیر لخت را داشته باشد. (در نظر داشته باشید که G و G معانی متفاوت دارند)

تانسور G اقتباس اینشتین از محاسبه‌ی انحنای ریمان است؛ این امر به طور کلی بستگی دارد به ارتباط تانسور متریک فضا-زمان و مشتقات آن. تانسور T همه‌ی اطلاعات لازم درباره‌ی منبع گرانش را به وسیله‌ی مشخص کردن توزیع انرژی و ماده، تأمین می‌کند. بنابراین، معادله میدان هندسه را در طرف چپ و گرانش را در طرف راست نشان می‌دهد. در نظر گرفتن یک منبع گرانش (T) و این معادله، تانسور G و در نهایت هندسه را بر حسب تانسور متر یک فضا و زمان g به اینشتین می دهد.

در معادلات میدان اینشتین، گرانش هندسه را معین می‌کند و بدون شگفتی، هندسه‌ی حرکت را معین می‌کند. اینشتین با ادامه‌ی استدلال فیزیکی‌اش، معادله‌ی تعمیم یافته‌ای از حرکت استخراج کرد، که جزء ریاضی اصلی‌اش ضرورت تانسور متریک فضا زمان g است. بنابراین توالی کل محاسبه به صورت زیر است

منبع گرانش → انحنا → تانسور متریک g → معادله‌ی حرکت

منبع گرانش با Tو انحنا با G بیان می شود، تانسور متریک از G استخراج و معادله حرکت با g معین می‌شود. به طور صریح و بی ابهام این یک راه نقل داستان نسبیت عام اینشتین است. توجه داشته باشید، که در این مورد ذکری از نیروها به میان نیامده است؛ هندسه رابطه‌ی بین گرانش و حرکت است و به همین دلیل عنوان این بخش را نیزفیزیک در حکم هندسه نام‌گذاری کردیم.

هندسه آن طور که از معادله‌ی میدان اینشتین آشکار می‌شود، اگر گرانش موجود باشد، همیشه به معنی انحنای فضایی یا هندسه‌ی غیراقلیدسی است. اما به جز در موارد خاص (به عنوان مثال؛ سیاهچاله‌ها) دامنه‌ی انحنا فوق‌العاده کوچک است. ریچارد فاینمن با استفاده از نظریه اینشتین برآورد می‌کند که فرمول اقلیدسی (مساحت سطح کره) برای محاسبه‌ی مساحت سطح کره‌ای با شعاع r به قدر ۱٫۳ قسمت در میلیون، در میدان گرانشی شدید در سطح خورشید، اشتباه است!

اینشتین دو کاربرد به عنوان امتحان‌هایی برای اعتبار نظريه‌ی عامش پیشنهاد کرد. یکی محاسبه‌ی خمیدگی پرتوهای نور نزدیک به خورشید، که بعدها به وسیله‌ی هیئت‌های اعزامی مشهور ادینگتون و کروملین تأیید شد. دیگری محاسبه‌ی مدار عطارد بود، که نشان می‌داد بنا به اقتضای نظریه‌ی نیوتون ثابت نیست، اما جهت‌گیری آن به کندی با آهنگ ۴۲٫۹ ثانیه قوسی در یک قرن تغییر می‌کند. این اثر رصد شده بود و اندازه ۴۳٫۵ ثانیه را نشان می‌داد. وقتی اینشتین موفقیت نظریه‌اش را دید به وجد آمد. او به یکی از دوستانش نوشت؛ به مدت چند روز از شدت هیجان از خود بیخود بودم.

پایس متذکر می شود، از آن زمان او می دانست؛ که طبیعت سخن گفته است، او باید دقیق باشد!

به جای مانده از قبل

در خلال بحث نسبیت، موضوعی به عنوان پرتوهای کاتدی مطرح شد، همان طور که آنجا ذکر کردم، برای فاصله نیفتادن میان بحث جذاب و متوالی نسبیت، قرار بر این شد که در پایان بحث گریزی به موضوع پرتوهای کاتدی و اشعه‌ ایکس و الکترون‌ها و مطالب مرتبط با آن بزنیم. پس شاید بد نباشد، در پایان این مقاله نسبتا طولانی، این قسمت را با بررسی این موضوع به پایان برسانیم.

پرتوهای کاتدی، اشعه‌ ایکس و الکترون‌ها

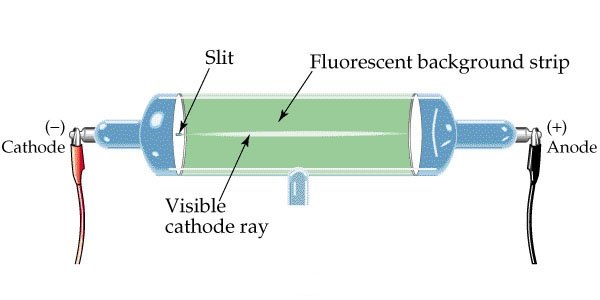
در سال ۱۸۷۷ میلادی ویلیام کروکس (۱۹۱۹-۱۸۳۲ میلادی) لامپ‌های تخلیه‌ای با فشار گاز بسیار پائین ساخت و نشان داد که پرتو کاتدی، ذرات بارداری است که به وسیله میدان مغناطیسی منحرف می‌شوند.

در سال ۱۹۸۵ میلادی ویلیام رونتگن با لامپ کروکسی که خود ساخته بود، آزمایشاتی انجام داد. او پرتو حاصل از لامپ را روی یک سطح که با ماده‌ی شیمیایی فسفرسانس پوشیده شده بود، تاباند و متوجه تابش سبزگونه ضعیفی از آن شد. او در سر راه این سطح و لامپ اجسام مختلفی قرار داد، ولی تابش سبز گونه هم چنان می‌درخشید و این اجسام بر آن تأثیر نداشتند. رونتگن متوجه شد، که لامپ تشعشع جدیدی که برای او ناشناخته بود، منتشر می‌کند. او اسم آن را به علت ناشناخته بودنش، پرتو ایکس نامید و در ادامه آزمایش با این پرتو، متوجه شد که اگر فیلم عکاسی، حتی اگر در لفاف کدری پوشیده شده باشد و در معرض این پرتو قرار گیرد، سیاه می شود. رونتگن دست خود را بین فیلم عکاسی و اشعه قرار داد و اثر استخوان‌های دستش را که روی فیلم ثبت شده بود مشاهده کرد. این کشف اهمیت زیادی در علم پزشکی برای تعیین شکستگی‌ها و وجود اجسام خارجی در بدن یافت. کشف رونتگن اثرات زیادی در پیشرفت‌های بعدی فیزیک داشت.

پژوهش‌های بیشتر در مورد ماهیت این پرتو نشان داد، که این پرتوها مشابه امواج الكترومغناطیسی بوده و مانند پرتوهای کاتدی باردار نبوده و نظیر نور پراشیده می‌شوند. این پرتوها به علت طول موج بسیار کوچک، برای پراشیده شدن به مانع‌های بسیار ریز نیاز داشتند. برای اندازه گیری طول موج پرتو ایکس از بلورهایی با فاصله سطوح اتمی کوچک استفاده شد. بعدها این روش و با استفاده از پرتو ایکس با طول موج مشخص برای تعیین ساختمان اتمی بلورها به کار گرفته شد. روش پراش اشعه ایکس امروز مهم ترین ابزار برای تعیین ساختار مولکولی و اتمی بلورها و مواد غیر بلوری است.

قبلا گفتیم که آزمایشات سِر جی. جی. تامسون نشان می‌داد، که پرتو کاتدی شاهدی بر پرتوهای الکترونی است و این پرتو به وسیله میدان‌های الکتریکی و مغناطیسی منحرف می‌شود. تامسون به کمک میدان‌های الکتریکی و مغناطیسی این پرتوها را منحرف کرد و راه پیدا کردن نسبت بار به جرم این ذرات ( e/m ) را یافت. تامسون دریافت این نسبت برای کلیه‌ی گازهای به کار رفته در لامپ‌های تخلیه گازی یکسان است.

در سال ۱۹۰۹ میلادی رابرت.ای. میلیكان ( ۱۹۵۳-۱۸۹۸ میلادی) به طور تجربی نشان داد که پرتوهای کاتدی فقط در واحد یا بسته های جدا وجود دارند. او این کار را با متوازن کردن وزن قطرات روغن باردار بین صفحات موازی یک خازن باردار در مقابل نیروهای الکتریکی که بین این صفحات به ذرات وارد می‌شد به اثبات رساند و با اندازه‌گیری وزن چندین قطره روغن و نیروهای الکتریکی وارد بر آن‌ها نشان داد، که بار الکتریکی این قطرات کوانتیده است، به طور تجربی نشان داده شد که تقریبا 6.242 × 1018 الکترون باری برابر یک کولن دارند. بنابراین بار هر الکترون 1.6× 10(1/10)  کولن است.

الكترون‌ها کوچک‌ترین بار الکتریکی شناخته شده در طبیعت هستند. فیزیکدانان نظری عقیده دارند، بارهایی برابر با ۱/۳  بار الکترون که کوارک‌ها نامیده می شوند، در طبیعت وجود دارد.

 چند ویژگی دیگر الكترون‌ها چنین است:

 ١) جرم الكترون‌ها ۱/۱۸۳۶ جرم پروتون و برابر با  9.11 × 31(1/10) کیلوگرم است.

٢) این ذره در میدان‌های الکتریکی و مغناطیسی منحرف می‌شود.

٣) اگر این ذرات را شتاب بدهیم، از خود تشعشع الكترومغناطیسی گسیل می‌کنند.

۴) در شتاب‌های بالا این تابش به شکل پرتو ایکس است.

 تامسون برای اندازه گیری نسبت e/m پرتو کاتدی را از میان، صفحات موازی باردار عمود بر هم که درون لامپ تخلیه قرار گرفته بودند، عبور داد. او با قرار دادن دو پیچک مغناطیسی عمود بر صفحات الکتریکی موازی می‌توانست پرتوها را منحرف کند. با انتخاب جهت مناسب جریان عبوری از پیچک‌ها می توان جهت انحراف پرتوهای کاتدی را در جهت خلاف انحراف به وسیله‌ی میدان الکتریکی صفحات موازی باردار که پرتو از داخل آن می گذرد تنظیم کرد. نیروی مغناطیسی وارد بر الکترون‌ها بستگی به بار و سرعت الکترون‌ها و شدت میدان مغناطیسی دارد. تامسون با اعمال میدان‌های الکتریکی و مغناطیسی و تنظیم انحرافها توانست مقدار e/m را به دست آورد.